Table of contents
Open Table of contents
What is Data Encryption Standard (DES)
The Data Encryption Standard (DES) is a method proposed by the National Bureau Standard (NBS) in 1976, which is now known as the National Institute of Standards and Technology (NIST) [5]. DES is a block cipher that uses a symmetric key capable of encrypting a 64-bit message. Symmetric key means that only one key is used in both the encryption and decryption processes. The following is the algorithm used to encrypt a text using DES.
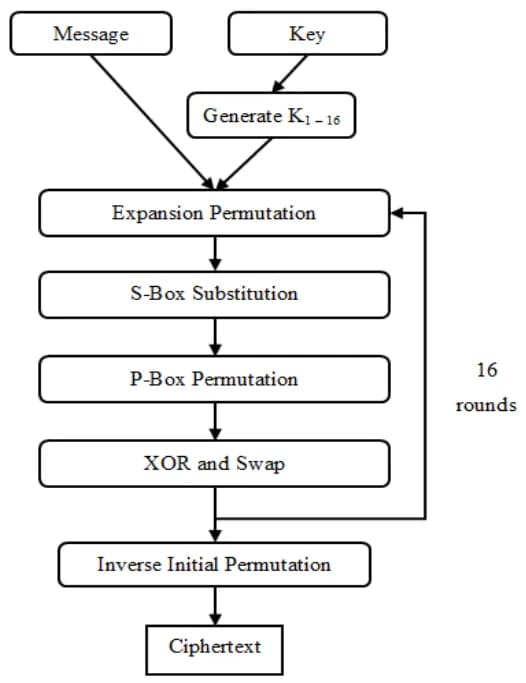
To encrypt a 64-bit message, DES performs a total of 16 rounds.
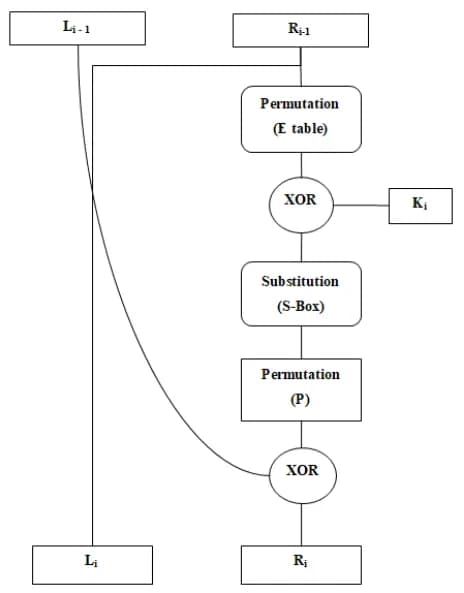
During each round, the process will divide the 64-bit message into two parts: left (L) and right (R), each 32 bits long. These two parts will undergo processing for a total of 16 rounds. Additionally, in the DES process, there is a key generation process that generates 16 different keys used for encryption in each round.
Implementation in Python
KEY
Change key to binary
The first step is to generate keys by converting the key into binary bits. Since the key is represented in capital alphabet letters, ASCII table is used for the conversion to binary.
key = input("Enter Key : ")
binary_result = ''.join(format(ord(char), '08b') for char in key)Result
# Key = DINUSIAN
['01000100', '01001001', '01001110', '01010101', '01010011', '01001001', '01000001', '01001110']Permutation using PC-1 table
Once the key bits are obtained, the PC-1 table is used to permute them with the key bits.
# PC-1 table
PC_1 = [57, 49, 41, 33, 25, 17, 9,
1, 58, 50, 42, 34, 26, 18,
10, 2, 59, 51, 43, 35, 27,
19, 11, 3, 60, 52, 44, 36,
63, 55, 47, 39, 31, 23, 15,
7, 62, 54, 46, 38, 30, 22,
14, 6, 61, 53, 45, 37, 29,
21, 13, 5, 28, 20, 12, 4]The permutation process is carried out by selecting key bits according to the indices in the PC-1 table. For example, if the first cell in the PC-1 table contains the number 57, then find the 57th bit in the key.

# Perform permutation using obtained bits
permuted_key = ''.join(binary_result[i - 1] for i in PC_1)Result
['0000000', '0111111', '1100000', '0000001', '1001010', '0100011', '0110100', '1101000']Split the permutation result
The permutation process with the PC-1 table will result in a 56-bit internal key. After that, split this internal key into two parts, namely C0 and D0, where each part has a length of 28 bits.
half_length = len(permuted_key) // 2
C0 = permuted_key[:half_length]
D0 = permuted_key[half_length:]Result
C0: ['0000000', '0111111', '1100000', '0000001']
D0: ['1001010', '0100011', '0110100', '1101000']Bit shift
Once C0 and D0 are obtained, perform left circular shifts (bit shift to the left) 16 times, with the number of bit shifts in each iteration according to the table below.

shift_left = [1, 1, 2, 2, 2, 2, 2, 2,
1, 2, 2, 2, 2, 2, 2, 1]
# Store the Ci + Di
array_permuted_key = []
# Perform bit shifts
for i in range(16):
# Extract the first bit and append it to the end
C0 = C0[shift_left[i]:] + C0[:shift_left[i]]
D0 = D0[shift_left[i]:] + D0[:shift_left[i]]
print(f"\n==== SHIFT {i+1} ====")
print(f"C-{i+1}:", separate_string(C0, 7))
print(f"D-{i+1}:", separate_string(D0, 7))The shift is performed by taking the last bit and placing it at the far left according to the specified number of shifts. For example, for shifting bits from C0:

Then, to determine the next value of C, shift the previous C value. For instance, to determine the value of C3, shift the bits from the C2 value according to the number of bit shifts in the table above.
Result
==== SHIFT 1 ====
C-1: ['0000000', '1111111', '1000000', '0000010']
D-1: ['0010100', '1000110', '1101001', '1010001']
==== SHIFT 2 ====
C-2: ['0000001', '1111111', '0000000', '0000100']
D-2: ['0101001', '0001101', '1010011', '0100010']
==== SHIFT 3 ====
C-3: ['0000111', '1111100', '0000000', '0010000']
D-3: ['0100100', '0110110', '1001101', '0001001']
==== ALL REMAINING SHIFT ====Combine Ci and Di
Then, the combination of Ci and Di forms CiDi.
for i in range(16):
C0 = C0[shift_left[i]:] + C0[:shift_left[i]]
D0 = D0[shift_left[i]:] + D0[:shift_left[i]]
print(f"\n==== SHIFT {i+1} ====")
print(f"C-{i+1}:", separate_string(C0, 7))
print(f"D-{i+1}:", separate_string(D0, 7))
# Add this code
CD = C0 + D0
CD_no_space = CD.replace(" ", "")
print(f"CD-{i+1}:", separate_string(CD_no_space, 7))Result
==== SHIFT 1 ====
...
CD-1: ['0000000', '1111111', '1000000', '0000010', '0010100', '1000110', '1101001', '1010001']
==== SHIFT 2 ====
...
CD-2: ['0000001', '1111111', '0000000', '0000100', '0101001', '0001101', '1010011', '0100010']
==== SHIFT 3 ====
...
CD-3: ['0000111', '1111100', '0000000', '0010000', '0100100', '0110110', '1001101', '0001001']
==== ALL REMAINING SHIFT ====Permute CDi with PC-2 Table
After combining into pairs (CDi), permute each pair using the PC-2 table below to form 16 keys (K1 – K16).
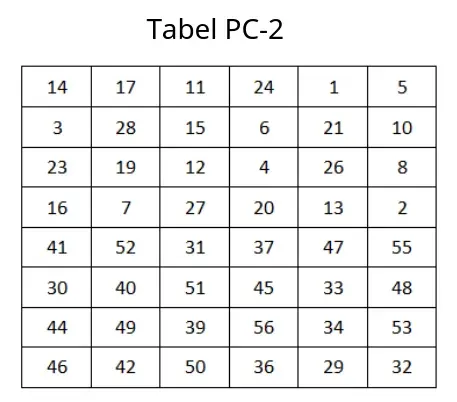
# PC-2 Table
PC_2 = [14, 17, 11, 24, 1, 5, 3, 28,
15, 6, 21, 10, 23, 19, 12, 4,
26, 8, 16, 7, 27, 20, 13, 2,
41, 52, 31, 37, 47, 55, 30, 40,
51, 45, 33, 48, 44, 49, 39, 56,
34, 53, 46, 42, 50, 36, 29, 32]
for i in range(16):
C0 = C0[shift_left[i]:] + C0[:shift_left[i]]
D0 = D0[shift_left[i]:] + D0[:shift_left[i]]
print(f"\n==== SHIFT {i+1} ====")
print(f"C-{i+1}:", separate_string(C0, 7))
print(f"D-{i+1}:", separate_string(D0, 7))
CD = C0 + D0
CD_no_space = CD.replace(" ", "")
print(f"CD-{i+1}:", separate_string(CD_no_space, 7))
# Add this code
# Perform permutation using PC-2
permuted_CD = ''.join(CD_no_space[i - 1] for i in PC_2)
# Store the result
array_permuted_key.append(permuted_CD)
print(f"K-{i+1}:", separate_string(permuted_CD, 6))Result
==== SHIFT 1 ====
...
K-1: ['101000', '001001', '001001', '001010', '111000', '010010', '110100', '101100']
==== SHIFT 2 ====
...
K-2: ['101000', '000001', '001011', '010010', '000001', '111101', '011000', '010001']
==== SHIFT 3 ====
...
K-3: ['001101', '000101', '001001', '010000', '100110', '110010', '010101', '100000']
==== ALL REMAINING SHIFT ====After each pair CDi is permuted with the PC-2 table, it will result in 16 keys as shown below:
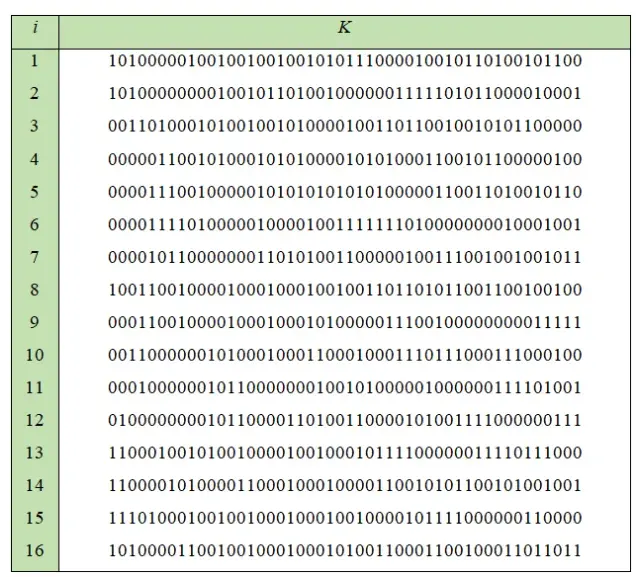
PLAINTEXT
Change plaintext to binary
Once the 16 keys are obtained from the key generation process, the next step is to process the message that will be encrypted.
# Plaintext = TUGUMUDA
plaintext = input("Enter Plaintext : ")
plaintext_binary = ''.join(format(ord(char), '08b') for char in plaintext)Result
['01010100', '01010101', '01000111', '01010101', '01001101', '01010101', '01000100', '01000001']Permute with IP-1 Table
IP_1 = [58, 50, 42, 34, 26, 18, 10, 2,
60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6,
64, 56, 48, 40, 32, 24, 16, 8,
57, 49, 41, 33, 25, 17, 9, 1,
59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5,
63, 55, 47, 39, 31, 23, 15, 7]
IP_1_result = ''.join(plaintext_binary[i - 1] for i in IP_1)Result
['11111111', '00101011', '01111111', '10111110', '00000000', '00000000', '00010000', '00000100']Split to L0 and R0
The new binary string will be divided into two parts: L0 (left) and R0 (right), each 32 bits long.
half_length_ip1 = len(IP_1_result) // 2
L0 = IP_1_result[:half_length_ip1]
R0 = IP_1_result[half_length_ip1:]Result
L0: ['11111111', '00101011', '01111111', '10111110']
R0: ['00000000', '00000000', '00010000', '00000100']Feistel Network (my brain not brained)
After that, use the Feistel network equation below to process L0 (left) and R0 (right) for a total of 16 rounds.
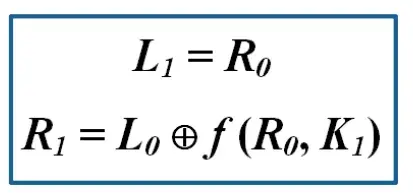
With Feistel Network, we know Li result is previous Ri result. Meanwhile, to obtain the value of R1, the first step is to process the function f, where the value of R0 will be permuted using the E-table.
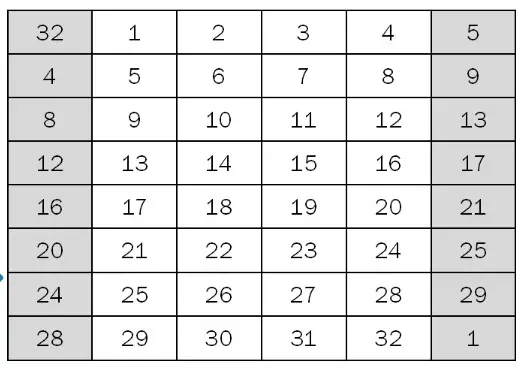
The E-table will expand (enlarge) R0, originally 32 bits, into 48 bits. Thus, the value of E(R0) is obtained as follows:
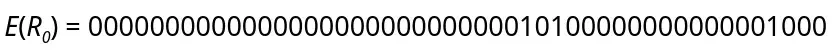
Next, implement the XOR operator between E(R0) and K1.

S Boxes
The next step is to divide the bits of the XOR result into blocks of 6 bits each, resulting in 8 blocks. Each of these blocks will be processed using an S-box, and in DES, there are 8 S-box tables for each block.
S_boxes = [
[
[14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7],
[0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8],
[4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0],
[15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13]
],
[
[15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10],
[3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5],
[0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15],
[13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9]
],
[
[10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8],
[13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1],
[13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7],
[1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12]
],
[
[7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15],
[13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9],
[10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4],
[3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14]
],
[
[2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9],
[14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6],
[4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14],
[11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3]
],
[
[12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11],
[10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8],
[9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6],
[4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13]
],
[
[4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1],
[13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6],
[1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2],
[6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12]
],
[
[13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7],
[1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2],
[7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8],
[2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11]
]
]Then, take the first and last bits from the block and separate them from the middle part. After dividing into 2 parts, the 2 bits (red bits) represent the row of the S-box, while the 4 bits (black bits) represent the column of the S-box.
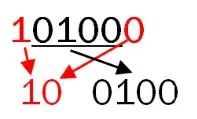
Thus, the intersection between the row and column will be the next value.
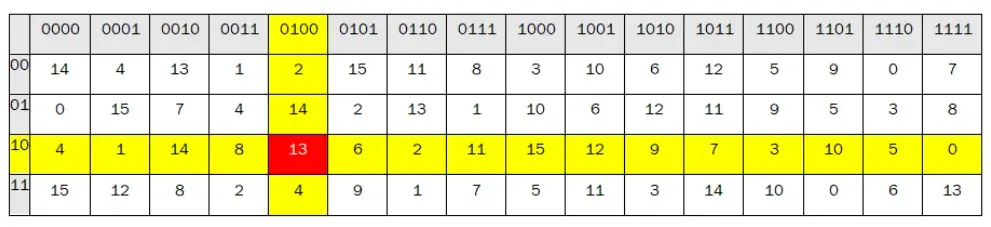
In the table above, the intersection between the row and column determined by the XOR result block shows the number 13. After that, convert this number into a 4-bit binary form, which is 13 = 1101.
Permute with P table
After obtaining the result from the S-box process, permute this result with the P-function table below:
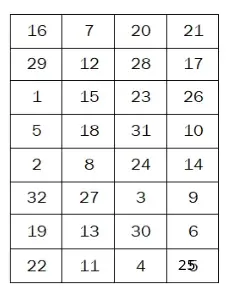
P = [16, 7, 20, 21, 29, 12, 28, 17,
1, 15, 23, 26, 5, 18, 31, 10,
2, 8, 24, 14, 32, 27, 3, 9,
19, 13, 30, 6, 22, 11, 4, 25]The result of permuting the S-box result with the P-function table will yield the value of f(R0, K1) as follows:
f (R0, K1) = 01100100110110001101010010110110Then, according to the equation to form the value of R1:
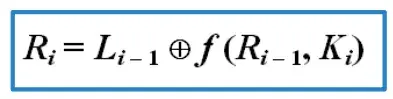
The block f(R0, K1) will be XORed with the block L0, so the value of R1 is:

Repeat the steps sequentially for a total of 16 rounds using all available keys (K1 – K16).
# R16 and L16 result
R16 = 00010010010000000011000110110111
L16 = 01110111100100110111100111100010Code time!
L_previous = L0
R_previous = R0
for i in range(16):
print(f"\n==== ROUND {i+1} ====")
print(f"L-{i+1}:", separate_string(R_previous, 8))
expanded_R = ''.join(R_previous[i - 1] for i in E)
print(f"E(R-{i+1}):", separate_string(expanded_R, 6))
R_xor_key = bin(int(expanded_R, 2) ^ int(array_permuted_key[i], 2))[2:].zfill(48)
print(f"XOR-{i+1}:", separate_string(R_xor_key, 6))
R_substituted = ''
for j in range(8):
block = R_xor_key[j * 6: (j + 1) * 6]
row = int(block[0] + block[5], 2)
col = int(block[1:5], 2)
substituted_value = format(S_boxes[j][row][col], '04b')
R_substituted += substituted_value
R_permuted = ''.join(R_substituted[i - 1] for i in P)
R_xor_L = bin(int(R_permuted, 2) ^ int(L_previous, 2))[2:].zfill(32)
L_previous = R_previous
R_previous = R_xor_L
print(f"L-{i + 1}:", separate_string(L_previous, 4))
print(f"R-{i + 1}:", separate_string(R_previous, 4))Result
==== ROUND 1 ====
L-1: ['00000000', '00000000', '00010000', '00000100']
E(R-1): ['000000', '000000', '000000', '000000', '000010', '100000', '000000', '001000']
XOR-1: ['101000', '001001', '001001', '001010', '111010', '110010', '110100', '100100']
L-1: ['0000', '0000', '0000', '0000', '0001', '0000', '0000', '0100']
R-1: ['1001', '1011', '1111', '0011', '1010', '1011', '0000', '1000']
==== ROUND 2 ====
L-2: ['10011011', '11110011', '10101011', '00001000']
E(R-2): ['010011', '110111', '111110', '100111', '110101', '010110', '100001', '010001']
XOR-2: ['111011', '110110', '110101', '110101', '110100', '101011', '111001', '000000']
L-2: ['1001', '1011', '1111', '0011', '1010', '1011', '0000', '1000']
R-2: ['1100', '1001', '0001', '0101', '0010', '1101', '0011', '1001']
...
==== ROUND 16 ====
L-16: ['01110111', '10010011', '01111001', '11100010']
E(R-16): ['001110', '101111', '110010', '100110', '101111', '110011', '111100', '000100']
XOR-16: ['100110', '110110', '111010', '000100', '001001', '111111', '011111', '011111']
L-16: ['0111', '0111', '1001', '0011', '0111', '1001', '1110', '0010']
R-16: ['0001', '0010', '0100', '0000', '0011', '0001', '1011', '0111']Conclusion
In summary, I set out to see if we could use Python for DES, drawing on what I’ve been learning in my cryptography course at university. Turns out, Python fits right into the picture. This journey highlights how practical coding can meet academic insights, making cybersecurity more accessible and exciting.
Regrettably, I couldn’t get my hands on the decryption material for DES this time. But, if I manage to snag it in the future, I’ll definitely whip up another post to share the scoop.